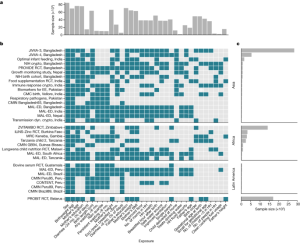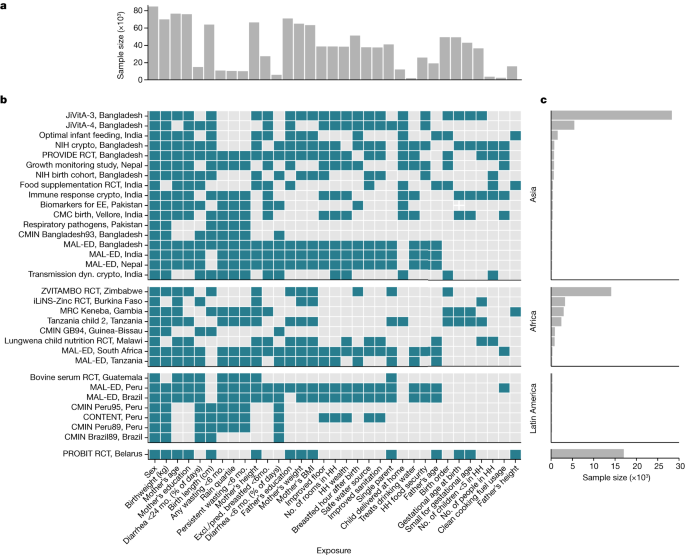
There are causes and consequences of child growth faltering

Estimating linear growth velocity vs. mean z-scores across cohorts and geographic regions using pooled spline curves

We estimated linear growth velocity within 3-month age intervals stratified by sex, pooling across study cohorts (Fig. 5) as well as stratified by geographic region (Extended Data Fig. 10) and study cohort (Supplementary Note 7.4). Analyses included cohorts that measured children at least quarterly. We included each measure within a 2 week window around the same age as the last one, to account for variation in the age. Random effects models for the primary analysis and fixed-effect models for sensitivity analyses were used in pooled analyses.

We classified countries into regions using the WHO categorization with the exception of Pakistan, which is consistent with previous studies using DHS20. We wanted to exclude it from the analyses because it was the only European study.

Mean z-scores by continuous age, stratified by levels of exposures from birth to 24 months were fit within individual cohorts using cubic splines with the bandwidth chosen to minimize the median Akaike information criterion across cohorts61. For each exposure category, we put together estimates of the splines. We pooled spline curves across cohorts into a single prediction, offset by mean z-scores at one year, using random-effects models62.

We used the maximum-likelihood estimation to figure out how the mean, standard deviation and skewness of LAZ distributions differed by age. We fitted models according to cohort.

Random-effects models assume that the true population outcomes θ are normally distributed (θ ~ N(μ, τ2)), in which N indicates a normal distribution and θ has mean μ and variance τ2. The random-effects model is used to estimate outcomes in this study.

in which ({\bar{\theta }}_{w}) is the weighted mean outcome in the set of k included studies, and wi is a study-specific weight, defined as the inverse of the study-specific sampling variance vi. The estimate from study is i.

The pooled estimates were fit by using the restricted maximum-likelihood estimation. The pooling methods are explained in the accompanying article. All parameters were pooled directly using the cohort-specific estimates of the same parameter, except for population-attributable fractions. Pooled PAFs were calculated from random-effects pooled population intervention effects (PIEs), and pooled outcome prevalence in the population using the following formulas76:

To examine the distribution of LAZ among children with stunting reversal, we created subgroups of children who experienced stunting reversal at ages 3, 6, 9 and 12 months and then summarized the distribution of the children’s LAZ at ages 6, 9, 12 and 15 months. We used the ages of stunting reversal to estimate the mean difference in LAZ at older ages, and then used the confidence intervals to estimate the mean difference. Pooled analyses used random-effects models for the primary analysis and fixed-effects models for sensitivity analyses as described above.

The proportional reduction in cumulative incidence was considered to be the PAF if the entire population was exposed to an ideal low risk reference level. We estimated the PAF for the prevalence of stunting and wasting at birth, 6, and 24 months and cumulative incidence of stunting and wasting from birth to 24 months, 6 to 24 months, and from birth to 6 months. For each exposure, we chose the reference level as the category with the lowest risk of stunting or wasting.

The comparison levels of exposure are at birth, 6 months, and 24 months. The z-scores used were the measures taken closest to the age of interest and within 1 month of the age of interest, except for z-scores at birth which only included a child’s first measure recorded by 7 days after birth. We took mean differences between LAZ,WAZ, weight and length velocities.

The cumulative incidence ratios between comparison levels and the reference level were used for the incident start of outcomes between birth and 24 months and 6 and 6 months.

Optimal individualized intervention impact. We used a variable importance measure methodology to estimate the impact of an optimal individualized intervention on an exposure63. The Optimal Intervention on an Exposure was determined through estimating individualized treatment regimes in which an individual-specific rule is given for the lowest-risk level of exposure. The same covariates are used to estimate the low-risk level as they are used to adjust for it. The impact of the optimal individualized intervention is derived from the variable importance measure, which is the predicted change in the population mean outcome from the observed outcome if every child’s exposure was shifted to the optimal level. This is different from the PIE and PAF parameters in that we didn’t specify a reference level, this also means that it could vary among participants.

The framework we use to identify potential confounders for each exposure is directed acyclic graph. We did not adjust for characteristics that were assumed to be intermediate on the causal path between any exposure and the outcome, because while controlling for mediators may help adjust for unmeasured confounders in some conditions, it can also lead to collider bias66,67. Supplementary Note 1 has the lists of adjustment covariates used for each analysis. The cohort-specific estimates could have residual confound because founding was not measured in every cohort.

The complete-case approach only included children with exposure and measurement that were missing. We impute missing covariate values for additional covariates in adjusted analyses. Within each cohort, if there was <50% missingness in a covariate, we imputed missing measurements as the median (continuous variables) or mode (categorical variables) among all children, and analyses included an indicator variable for missingness in the adjustment set. The potential adjustment set excluded covariates with more than 50% missingness. When calculating the median for imputation, we used children as independent units rather than measurements so that children with more frequent measurements were not over-represented.

We figured out the influence of curve-based, clustered standard errors to account for the analyses of recovery from wasting or progression to severe wasting. The unit of independence in the original study was assumed to be the unit of clustering since it was the independent unit of analysis. We used clusters as the unit of independence for the iLiNS-Zinc, Jivita-3, Jivita-4, Probit, and SAS Complementary Feeding trials. The normal approximation was used to estimate the 85% confidence intervals for incidence.

If there were five or fewer cases in the reference group, we didn’t estimate the relative risks between the two groups. In such cases, we still estimated relative risks between other exposure strata and the reference strata if those strata were not sparse. For rare outcomes, we only included one covariate for every 10 observations in the sparsest combination of the exposure and outcome, choosing covariates based on ranked deviance ratios.

rmconfidence, rmInterval, rmOutcome.

For PAFs of exposures on the cumulative incidence of wasting and stunting, the pooled cumulative incidence was substituted for the outcome prevalence in the above equations. Unlike PAFs, PIEs are symmetrically confidence intervals and we used this method instead of direct pooling.

Mean trajectory estimates were made from individual studies and curves were pooled using random effects. The Curves are calculated from the anthropometry measurements of children taken from birth to 24 months of age and the measure of maternal anthropometry.