Revised historical records make sense on global warming
Turn-of-the-Twentieth-Century Climate Reconstruction for Co-Located Land and Coastline Grid Cells
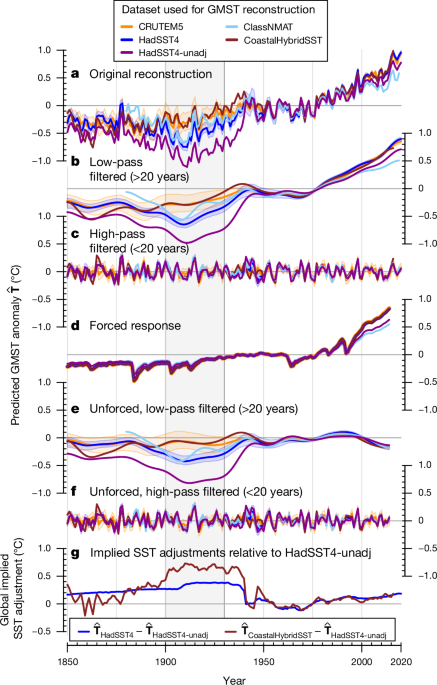
Turn-of-the-twentieth-century temperature change (1901–1920 averages compared with 1871–1890 averages). We compared the multidecadal period before the ocean cold anomalies with the cold anomalies, because ocean-derived temperatures deviate from the land-derived temperatures. Around the turn of the twentieth century we computed multidecadal temperature changes using the temperature average from both periods. These temperature differences are computed for co-located coastal SST and LSAT data (Fig. 3), and for the global reconstructions and palaeoclimate reconstructions (Fig. 4). For large-scale regions, a t-test for differences between co-located coastal land and coastal marine grid cells was conducted. 3c.
Our statistical model is to be trained from perturbed climate model patterns and to predict the unperturbed target metric. This yields a new set of regression coefficients based on the perturbed data (({\widehat{{\boldsymbol{\beta }}}}{{\rm{Land}}:1895\text{-}06}^{ {\rm{GMST}}}) and ({\widehat{{\boldsymbol{\beta }}}}_{{\rm{Ocean}}:1895\text{-}06}^{ {\rm{GMST}}})). By adding the error terms, the algorithm optimally predicts the target metric as in equations (1)–(5) while taking into account ‘real-world’ estimates of uncertainties and biases in the estimation of the regression coefficients. The coefficients are lowered for grid cells that are strongly affected by uncertainties and biases. Finally, following equations (4) and (5), we obtain observation-based reconstructions of each target metric (({\widehat{{\bf{T}}}}{{\rm{CRUTEM}}5}^{ {\rm{GMST}}}) and ({\widehat{{\bf{T}}}}_{{\rm{HadSST}}4}^{ {\rm{GMST}}})), and analogously based on CMIP6 models (({\widehat{{\bf{T}}}}{{\rm{CMIP}}6,{\rm{Land}}}^{ {\rm{GMST}}}) and ({\widehat{{\bf{T}}}}_{{\rm{CMIP}}6,{\rm{Ocean}}}^{ {\rm{GMST}}})). An ensemble of 200 observational reconstructed time series (({\widehat{{\bf{T}}}}{{\rm{CRUTEM}}5}^{ {\rm{GMST}}}) and ({\widehat{{\bf{T}}}}_{{\rm{HadSST}}4}^{ {\rm{GMST}}})) is thus obtained, where the input for each reconstruction contains a different error realization. The main text has the untarnished asterisks removed because all observations-based reconstructions are trained with bias and uncertainty realizations added to CMIP6. For the reconstructions of CMIP6: (WidehatBFT)_rmCMIP6,. Model members are treated as observations, meaning random error and bias realization is added to them. The reconstruction uncertainty ranges in Figures 1 and 2 are derived from the reconstructed ensemble, which is a statistical model from 200 different bias and uncertainty realizations. The performance of the statistical reconstruction on CMIP6 models was shown in an illustration as extended data fig. 3. Supplementary information gives an evaluation of the approach with uncertainties and biases.
where N is the number of available samples. The estimate of the regression slope is given by the minimization. The ‘prediction error’ of linear regression is given by44:
On the reconstruction of ocean- and land-based temperature charts from LSAT and SST data using a regularized linear regression method with ridge regression
The temperature difference is between the ocean and the land. We analysed the difference between the ocean- and land-based reconstructions at each time step for a given target metric, (\Delta {\hat{{\bf{T}}}}{{\rm{O}}\text{-}{\rm{L}}}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}}={\hat{{\bf{T}}}}{{\rm{H}}{\rm{a}}{\rm{d}}{\rm{S}}{\rm{S}}{\rm{T}}4}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}}-{\hat{{\bf{T}}}}_{{\rm{C}}{\rm{R}}{\rm{U}}{\rm{T}}{\rm{E}}{\rm{M}}5}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}}). The Delta widehatT_rmOtext-rmLrmGMST was compared with the equivalently masked reconstruction range of ocean and land temperatures.
To predict global temperature metrics from the LSAT or SST records with incomplete coverage, we invoked a regularized linear regression method known as ridge regression, a key tool in statistical learning23. Training of the statistical models was based on climate model simulations from the CMIP6 archive50 with complete coverage, from which we calculated the target metrics of the statistical model. We focus on GMST as the target metric, but we also reconstructed global mean land surface temperature and global mean sea surface temperature. The SSTs of the West Pacific, Indian Ocean and West Atlantic were reconstructed for the land data. The selected target metrics represent key metrics of global temperature change11 and regional ocean temperature change for the comparison with ocean palaeoclimate reconstructions33. The maps were drawn from the CRUTEM5 data and the HadSST4 data. The conceptual reconstruction set-up was done using a linear statistical model that relates incomplete spatial LSAT or SST patterns to the target metric.
To analyse our GMST reconstructions, we apply a timescale filtering and an attribution method in Fig. 1. The low-pass filter with a period of 20 years separated our original reconstruction in a high-pass and low-pass time series.
It is noted that despite the fact that the coverage is restricted to the June 1895 masks in this example, we still used all months of June in the full time period of 1850–2014 (partly extended to 2020) from the historical simulations of climate models for training the regression models (that is, the estimation of regression coefficients). The dimensions of (X_rmmod,rmLand:1895rmmbox–06) are n and p, respectively.
We obtained observation-based predictions for all target metrics by using the CRUTEM5 and HadSST4 data as inputs to the regression models. The comparison of our observation-based reconstruction with CMIP6 models in Fig. 2 was based on 602 CMIP6 historical simulations that contain ‘tas’ and ‘tos’ data, that is, 98.835 model-years (overview in Supplementary Table 4), which were masked and reconstructed with observational coverage for each time step.
We chose three historical ensemble members from each CMIP6 model and the time period from 1850 to 2020 to train our regression models. There was a training dataset consisting of 15,626 model-year, and an overview of the CMIP6 models used fortraining was given in Supplementary Table 4. As the optimal reconstruction coefficients may vary seasonally, training of the regression models for each month m was based on monthly data only from the same month in CMIP6 models (that is, the 15,626 model-years correspond to 15,626 monthly training samples).
We used the variables to be used as regression predictors, from the climate model historical (1509–14) and the simulation following the shared socio economic pathway (2-4) scenario. All simulations were redrawn to the same grid as the CRUTEM5 and HadSST4 grids. The data for the climate model was centred on a reference period from 1959 to 1990.
We used a standard cross-validation approach to determine the ridge regression parameter (λ) and to obtain the regression coefficients. In data science, it’s a common practice to split the data into different folds. This makes sure that fitting and validation happen on different data subsets. The iterative perfect model approach used in climate science is similar to the leave one model out strategy used here. In this process, for a total of k CMIP6 models, the ridge regression model is iteratively fitted on k − 1 models and validated on the kth model (referred to as ‘leave-one-model-out cross-validation’). This iterative approach guarantees that the regression coefficients generalize effectively to an unseen model, ensuring the robustness of the statistical model across the CMIP6 multi-model archive. The tuning parameter λ is then selected during cross-validation to minimize the mean squared error on out-of-fold data, and the corresponding regression coefficients are extracted. The average across the k model is used to get the final set of regression coefficients. We weight the regression so that each model gets the same amount of weight as it gets for the regression coefficients.
This results in small yet non-zero regression coefficients, and these coefficients are relatively evenly distributed among correlated predictors23. The extent of shrinkage can be determined through cross-checking the tuning parameter. The intercept of the linear model is not shrunk.
bold symbolbeta mathoprmrrmg
The number of predictors can make a linear regression problem with a high dimensionality. Conventional methods such as ordinary least squares aim to minimize the residual sum of squares (({\rm{R}}{\rm{S}}{\rm{S}}={\sum }{i}^{n}{({{\bf{Y}}}{i}-{X}_{{\bf{i}}}{\boldsymbol{\beta }})}^{2})). However, in high-dimensional settings, relying on this single objective may be problematic because regression coefficients lack proper constraints53. Ridge regression is a technique designed for scenarios with collinearity issues. Ridge regression prevents overfitting by incorporating a penalty for model complexity through the shrinkage of regression coefficients. The degree of shrinkage is determined by the sum of squared regression coefficients and ridge regression parameters. ridge regression addresses a joint minimization problem.
Source: Early-twentieth-century cold bias in ocean surface temperature observations
Uncorrelated uncertainties in the CRUTEM5 data set: the HadSST4 ensemble for SST and LSAT anomalies and its application to coastal grid cells
$${\widehat{{\bf{T}}}}{{\rm{CRUTEM5}}:1895\text{-}06}^{{\rm{GMST}}}={X}{{\rm{CRUTEM5}}:1895\text{-}06}\,{\widehat{{\boldsymbol{\beta }}}}_{{\rm{Land}}:1895\text{-}06}^{{\rm{GMST}}},$$
In CRUTEM5, uncertainties are encoded following the method given in ref. 52. The HadCRUT5 Noninfilled Data Set13 has produced a 200 member ensemble of uncertainties that are temporally and spatially correlated. The HadSST4 ensemble has been used to unblend SST and LSAT anomalies in coastal grid cells. The ensemble realization of biases includes uncertainty in climatological normals as well as station-based homogeneity errors and non-standard sensor enclosures. 13,24,52). Uncorrelated uncertainties (measurement errors or incomplete sampling of grid cells) are available in the form of gridded error fields (that is, ϵu,Land(s, t)).
X_rmHadSSTText-06
For a given coverage mask, the training of our statistical reconstruction model was set up for both SSTs and LSATs.
X_rmmod,rmLand:1895text