Physicists observe quarks for the first time

First Observation of Entanglement in a Pair of Top-Antitop Quarks at (340,rmGeV)

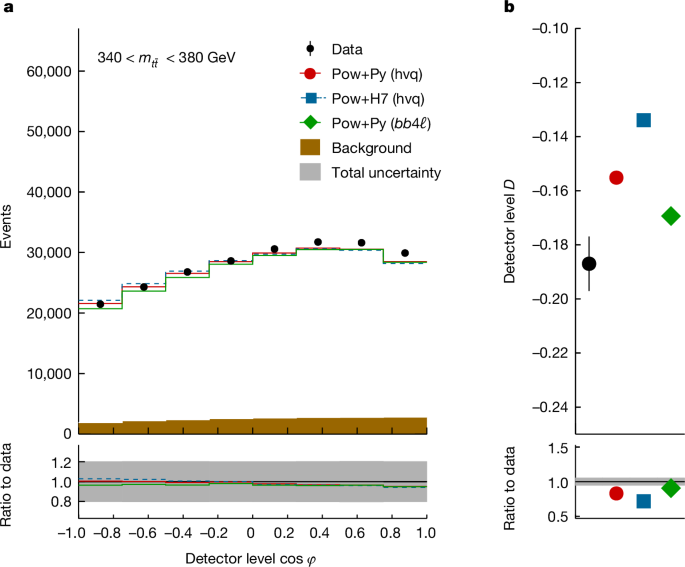
The Monte Carlo model is used to account for the fiducial phase space of the measurement, but it does not correspond to the observed and expected significances in the signal region. This is presented in a picture. In this case, the hypothesis of no interference is shown. The observed result in the region with (340\,{\rm{GeV}} < {m}_{t\bar{t}} < 380\,{\rm{GeV}}) establishes the formation of entangled (t\bar{t}) states. This constitutes the first observation of entanglement in a quark–antiquark pair.

Quarks are most commonly produced in hadron collider experiments as matter–antimatter pairs. A two-qubit system with the spin quantum state described by the spin density matrix is called a pair of top–antitop quarks.

$$ .

$$\rho =\frac{1}{4}\left[{I}{4}+\sum {i}\left({B}{i}^{+}{\sigma }^{i}\otimes {I}{2}+{B}{i}^{-}{I}{2}\otimes {\sigma }^{i}\right)+\sum {i,j}{C}{ij}{\sigma }^{i}\otimes {\sigma }^{j}\right].$$

Monte Carlo simulation of the top quarks’ (tbart) signals and decays in PYTHIA and HERWIG

The calibration procedure is performed in the signal region and the two validation regions to correct the data to a fiducial phase space at the particle level, as described in the previous section. All systematic uncertainties are included in the three regions. The expected results were observed.

Monte Carlo event simulations are used to model the (t\bar{t}) signal and the expected standard model background processes. The production of (tbart) events was modelled using a POWHeG box. The event were interfaced to either Pylai 8.30 or Herwig 7.2.10 in order to model the part. The top quarks’ decays were modeled at leading-order precision. An additional sample that generates (t\bar{t}) events at full NLO accuracy in production and decay was generated using the POWHEG BOX RES (bb4ℓ) (refs. A generator that is interfaced to PYTHIA. Further details of the setup and tuning of these generators are provided in the section ‘Monte Carlo simulation’. An important difference between PYTHIA and HERWIG is that the former uses a pT-ordered shower, whereas the latter uses an angular-ordered shower (see section ‘Parton shower and hadronization effects’). Full information on the spin density matrix isn’t passed to the parton shower programs, so it is not fully preserved during the shower.

Systematic Uncertainties and Their Impact on the POWHEG + PYTHIA Calculation: I. The Standard Model Prediction

A summary of the different sources of systematic uncertainty and their impact on the result is given in Table 1. The size of each systematic uncertainty depends on the value of D and is given in Table 1 for the standard model prediction, calculated with POWHEG + PYTHIA. The systematic uncertainties considered in the analysis are described in detail in the section ‘Systematic uncertainties’.

For all of the detector-related uncertainties, the particle-level quantity is not affected and only detector-level values change. In signal modelling uncertainties the effects at the particle level travel to the detector level, causing shifts in both levels. Uncertainties in modelling the background processes affect how much background is subtracted from the expected or observed data and can, therefore, cause changes in the calibration curve. These uncertainties are treated as fully correlated between the signal and background (that is, if a source of systematic uncertainty is expected to affect both the signal and background processes, this is estimated simultaneously and not separately).

The plotted pairs of (D_rmparticleprime ) and (D_rmDetectorprime ) are shown. 2a. There is a line between the points. Any value for Ddetector can be adjusted according to the particle level.

The standard model background processes that contribute to the analysis are the production of a single top quark with a W boson (tW), pair production of top quarks with an additional boson (t\bar{t}+X) (X = H, W, Z) and the production of dileptonic events from either one or two massive gauge bosons (W and Z bosons). The generators for the hard-scatter processes and the showering are listed in the section ‘Monte Carlo simulation’. For data and Monte Carlo events, the procedure for identifying and reconstructing detector-level objects is the same.

The background contribution of events with reconstructed objects that are misidentified as leptons, referred to as the ‘fake-lepton’ background, is estimated using a combination of Monte Carlo prediction and correction based on data. This data-driven correction is obtained from a control region dominated by fake leptons. It is defined by using the same selection criteria, but only if the two leptons have the same electric charges. The difference between the numbers of observed events and predicted events in this region is taken as a scale factor and applied to the predicted fake-lepton events in the signal region.

Only events taken during stable-beam conditions, and for which all relevant components of the detector were operational, are considered. To be selected events need to have one electron and one muon. At least one of the jets must be identified to be from a b-hadron.

The particle detector with a forward–backward symmetric cylindrical geometry and a solid-angle coverage is called the ATLAS experiment. It is used to record particles produced in LHC collisions through a combination of particle position and energy measurements. The coordinate system can be found in the section labeled “Object identification in the ATLAS detector”. It consists of an inner-tracking detector surrounded by a thin superconducting solenoid providing a 2 T axial magnetic field, electromagnetic and hadronic calorimeters, and a muon spectrometer. The muon spectrometer surrounds the calorimeters and is based on three large superconducting air-core toroidal magnets with eight coils each providing a field integral of between 2.0 T m and 6.0 T m across the detector. An extensive software suite40 is used in data simulation, the reconstruction and analysis of real and simulated data, detector operations, and the trigger and data acquisition systems of the experiment. A complete dataset of pp collision events with a centre of mass energy of 13 TeV is used to represent an integrated luminosity of 140 fb1. The analysis is focused on the data sample recorded.

The measurements are able to agree on predictions from different Monte Carlo setup within the uncertainties in the validation regions. This check is to verify the method used for the measurement.

The POW HEG generators give different predictions in the signal region. The size of the observed difference is consistent with different shower ordering methods and it is discussed in detail in the section that describes the hadronization effects.

Top-quark pair entanglement in high energy collisions: A perspective from the physicist on the theory of entangled quarks

Scientists have always said that top-quark pairs can be entangled. The current best theory of particle physics is built on quantum mechanics. But the latest measurement is nonetheless valuable, researchers say.

But the fact that entanglement hasn’t been rigorously explored at high energies is justification enough for Afik and the phenomenon’s other aficionados. “People have realized that you can now start to use hadron colliders and other types of colliders for doing these tests,” Howarth says.

The top quarks are what eventually made the proposal work. James Howarth, an experimental physicist in Glasgow, UK, who was part of the analysis, says that you cannot do this with lighter quarks. After only a short time, they start mixing with each other to form hadrons, so they dislike being separated. The top quark doesn’t have time to Hadronize or lose its spin information due to the fact it decays quickly. Instead, all of that information “gets transferred to its decay particles”, he adds. This means that the researchers can measure the decay products’ properties and infer the spin of the parent quarks.

The lives of the top and anti-top quarks can be infinitesimally short. They decay into longer-lived particles.

Source: Quantum feat: physicists observe entangled quarks for first time

Physicist Juan Felipe Saavedra: Entanglement at the CERN Large Hadron Collider (CMS)

Juan Felipe Saavedra is a theoretical physicist at the Institute of Theoretical Physics in Madrid. “Having an expected result must not prevent you from measuring things that are important.”

“It is really interesting because it’s the first time you can study entanglement at the highest possible energies obtained with the LHC,” says Giulia Negro, a particle physicist at Purdue University in West Lafayette, Indiana, who worked on the CMS analysis.