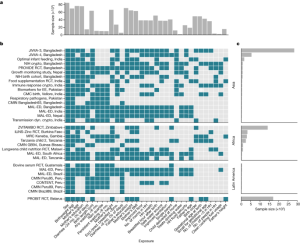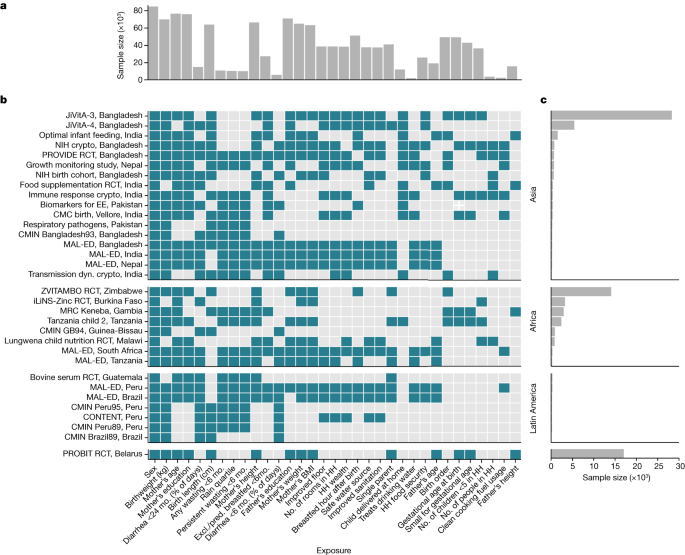
There are causes and consequences of child growth faltering

Statistical analysis of population-attributable fractions. I. Methodology and individual participant meta-analysis in South Asian, African and Latin American populations

Population-attributable fraction (PAF) was defined as the proportional reduction in cumulative incidence if the entire population’s exposure was set to an ideal low-risk reference level. Stunting and wasting can occur from birth to 6 months and then 24 months, 6 to 24 months, and finally from birth to 6 months. The reference level is the category with the lowest risk of stunting or wasting.

Further, persistent wasting was defined as a greater than 50% longitudinal prevalence of below- 2WLZ and a further more than 50% longitudinal prevalence of below 3WLZ.

The following are the outcomes of interest within each subgroup: child age, region of the world, and month of the year. The percentage of the country living on less than the United Nations Development Programme’s average is one of three country-level characteristics that we pooled by proportion. Within each country, in years without available data, we linearly interpolated values from the nearest years with available data and extrapolated values within five years of available data using linear regression models based on all available years of data.

A two stage individual participant meta-analysis was conducted by us where we estimated wasting outcomes and pooling estimates within each age group. We estimated each age-specific mean using a two-step process. We first estimated the mean in each cohort, and then pooled age-specific means across cohorts allowing for a cohort-level random effect. We estimated overall pooled effects for both South Asian, African and Latin American populations. Fixed-effects models are used in the pooling of all statistics presented in the figures. The pooling methods are described in greater detail in a companion paper19. The pooling was done using the rma function from the metaphor package in R language. Median durations were pooled across cohorts using the unweighted median of medians method60.

Comparing age-stratified LAZ,WAZ and WLZ over day of the year using TerraClimate and generalized cross-validation

Fitted smoothers used in the figures were fitted using cubic splines and generalized cross-validation61. We estimated simultaneous 95% CIs by using a bootstrap that was reanalyzed from the model and a matrix of covariance.

Child birthday and seasons are compared with the meanWLZ over day of the year. We assumed meanWLZ by cohort over day of the year and child’s birthday. Splines ofWLZ over day of the year were plotted and averaged over the years in which a study measured a child’s age at 24 months. We pulled monthly precipitation values from TerrraClimate, a dataset that combines readings from WorldClim data, CRU Ts4.0 and the Japanese 55-year Reanalysis Project64. For each study region, we averaged all readings within a 50-km radius from the study coordinates. We used the exact location of the cohort on the basis of published descriptions if gps locations weren’t included in the data. They matched the month with the calendar month and the year to look at the data.

Estimates were unadjusted for other covariates because we assumed that seasonal effects on WLZ were exogenous and could not be confounded. Mean differences in WLZ were pooled across cohorts using random-effects models, with cohorts grouped by the Walsh and Lawler seasonality index65. It was classified as occurring in locations with high seasonality if there’s an index greater than or equal to 0.9, if there’s an index less than or equal to 0.8, and if there’s an index less than or equal to 0.7.

We downloaded standard DHS individual recode files for each country from the DHS program website (https://dhsprogram.com/). We estimated age-stratified mean LAZ,WAZ andWLZ from ages 0 to 24 months within each DHS survey, using the most recent DHS datasets for individual women, household and length and weight from each country. See a companion paper for further details on the DHS data cleaning and analysis19. DHS estimates were compared with the mean LAZ, WAZ andWLZ by age in the Ki study cohort using a generalized cross-validation63. We didn’t change DHS measurement during the season.

The child was considered at risk of incident outcomes at birth if the exposures occurred before the baby was born. To estimate the relationship between household characteristics, paternal characteristics and child characteristics, we classify children who were born stunted as stunting or wasting.

We assessed the effects of covariate missingness by comparing results with median/mode missingness imputation to a complete-case analysis and examined covariate missingness by study. We compared adjusted estimates with estimates that were not adjusted, using random-effects models which are more conservative in the presence of heterogeneity, and estimates pooled using fixed effects which are more liberal in the presence of heterogeneity. We plotted a child growth trajectory for every exposure in Supplementary Note 5. We re-estimated the attributable differences of exposures on WLZ and LAZ at 24 months, dropping the PROBIT trial, the only European study (Supplementary Note 6). There is a plot of point estimates and confidence intervals from all the age, exposure and growth outcome combinations.

The prevalence ratios were compared to a reference level at birth, 6 months, and 24 months. Prevalence was estimated using anthropometry measurements closest to the age of interest and within one month of the age of interest, except for prevalence at birth which only included measures taken on the day of birth.

Unadjusted prevalence ratios and CIRs between the reference level of each exposure and comparison levels were estimated using logistic regressions69. The mean differences for continuous outcomes were estimated using linear regressions.

Mean z-scores by continuous age, stratified by levels of exposures from birth to 24 months were fit within individual cohorts using cubic splines with the bandwidth chosen to minimize the median Akaike information criterion across cohorts61. We estimated the numbers for each exposure category. We pooled curves across cohort into a single prediction that was offset by the mean z-score at one year.

The intervention impact is optimal. The variable importance measure methodology was used to estimate the impact of an intervention. The optimal intervention on an exposure was determined through estimating individualized treatment regimes, which give an individual-specific rule for the lowest-risk level of exposure based on individuals’ measured covariates. The covariates that were used to estimate the low-risk level are the same ones used for the adjustment in section 6 below. The impact of the optimal individualized intervention is derived from the variable importance measure, which is the predicted change in the population mean outcome from the observed outcome if every child’s exposure was shifted to the optimal level. This differs from the PIE and PAF parameters in that we did not specify the reference level; moreover, the reference level could vary across participants.

For each exposure, we used the directed acyclic graph framework to identify potential confounders from the broader set of exposures used in the analysis65. While controlling for mediators may help adjust for unmeasured confounders in some conditions, it can also lead to collider biases because of the assumed intermediate path between exposure and outcome. Detailed lists of adjustment covariates used for each analysis are available in Supplementary Note 1. Confounders were not measured in every cohort so there could be residual confound in estimates.

Analyses used a complete-case approach that only included children with non-missing exposure and outcome measurements. For additional covariates in adjusted analyses, we used the following approach to impute missing covariate values68. Within each cohort, if there was <50% missingness in a covariate, we imputed missing measurements as the median (continuous variables) or mode (categorical variables) among all children, and analyses included an indicator variable for missingness in the adjustment set. The potential adjustment set excludes covariates that have more than 50% missingness. Children were used as independent units instead of measurements in order to limit the representation of children with more frequent measurements.

If there were 5 cases in either the first or second levels, we did not estimate relative risks between a higher level of exposure and the reference group. We continued to estimate relative risks between the exposure strata and the reference one if there were more of them. For rare outcomes, we only included one covariate for every 10 observations in the sparsest combination of the exposure and outcome, choosing covariates based on ranked deviance ratios.

A non direct pooling of PAFs based on cumulative incidence of wasting and stunting: A $rmPAF,95%,Rm Confidence Interval=

$${\rm{PAF}}\,95 \% \,{\rm{confidence}}\,{\rm{interval}}=\frac{{\rm{PIE}}\,95 \% \,{\rm{confidence}}\,{\rm{interval}}}{{\rm{Outcome}}\,{\rm{prevalence}}}\times 100$$

For PAFs of exposures on the cumulative incidence of wasting and stunting, the pooled cumulative incidence was substituted for the outcome prevalence in the above equations. Unlike PAFs, PIEs are not direct pooling because of their symmetrical confidence intervals.